Рабочий лист 09.12. -7 кл геом
Дорогие ученики! Ознакомьтесь, пожалуйста, с предложенными материалами и заданиями, выполните их. Желаю вам успешного освоения материала!
Ход уроков
1. Посмотрите видеоуроки
Окружность. Построение циркулем и линейкой. https://clck.ru/SMvfp
Примеры задач на построение Теория и практика. https://clck.ru/S3tfK
2. Выполните предложенные задания на сайте ДО
Геометрия 7 « А, Б, В, Д, Е » Окружность. Построение циркулем и линейкой. Примеры задач на построение. (2урока)
Навигация (только номера заданий)
0 из 11 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
Информация
Ознакомьтесь, пожалуйста, с предложенными материалами и заданиями, выполните их. Желаю вам успешного освоения материала!
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается...
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Результаты
Правильных ответов: 0 из 11
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Нет рубрики 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- С ответом
- С отметкой о просмотре
-
Задание 1 из 11
1.
Количество баллов: 1Вставить пропущенное слово. … — геометрическая фигура, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от данной точки.
Правильно
Неправильно
Подсказка
Окружность
-
Задание 2 из 11
2.
Количество баллов: 1… — это отрезок, соединяющий центр окружности с любой точкой окружности. Из определения следует, что можно провести бесконечное количество радиусов, и они все имеют одинаковую длину.
Правильно
Неправильно
Подсказка
Радиус
-
Задание 3 из 11
3.
Количество баллов: 1Центром окружности является а) точка, от которой одинаково удалены некоторые точки; б) точка, от которой одинаково удалены все точки окружности.
Правильно
Неправильно
-
Задание 4 из 11
4.
Количество баллов: 1Хордой окружности называется а) отрезок, соединяющий две любые точки окружности; б) отрезок, соединяющий две любые точки.
Правильно
Неправильно
-
Задание 5 из 11
5.
Количество баллов: 1Диаметром окружности называется а) прямая, проходящая через центр окружности; б) хорда, проходящая через центр окружности.
Правильно
Неправильно
-
Задание 6 из 11
6.
Количество баллов: 1Указать проведенные радиусы окружности
Правильно
Неправильно
-
Задание 7 из 11
7.
Количество баллов: 1Указать хорды на окружности
Правильно
Неправильно
-
Задание 8 из 11
8.
Количество баллов: 1Установить последовательность шагов .
Отложить от данного луча угол, равный данному.
-
Проведем произвольную окружность с центром в вершине А данного угла. Пусть В и С — точки пересечения окружности со сторонами угла
-
Радиусом АВ проведем окружность с центром в точке О — начальной точке данного луча
-
Точку пересечения этой окружности с данным лучом обозначим С1.
-
Опишем окружность с центром С1 и радиусом ВС. Точка В1 пересечения двух окружностей лежит на стороне искомого угла. Это следует из равенства Δ ABC = Δ ОВ1С1 (третий признак равенства треугольников).
Правильно
Неправильно
-
-
Задание 9 из 11
9.
Количество баллов: 1Установить последовательность шагов.
Построить биссектрису данного угла
-
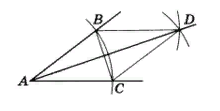
Из вершины А данного угла, как из центра, проводим окружность произвольного радиуса.
-
Пусть В и С — точки ее пересечения со сторонами угла. Из точек В и С тем же радиусом описываем окружности.
-
Пусть D — точка их пересечения, отличная от А.
-
Луч AD делит угол А пополам. Это следует из равенства Δ ABD = Δ ACD (третий признак равенства треугольников).
Правильно
Неправильно
-
-
Задание 10 из 11
10.
Количество баллов: 1Установить последовательность шагов.
Построить середину данного отрезка АВ..
-
Произвольным, но одинаковым раствором циркуля (большим 1/2 АВ)
-
описываем две дуги с центрами в точках А и В,
-
Точки пересечения окружностей обозначим точками C и D
-
Проведем отрезок через точки C и D
-
Каждая из точек С и D одинаково удалена от А и В
-
Следовательно, отрезок CD делит пополам отрезку АВ.
Правильно
Неправильно
-
-
Задание 11 из 11
11.
Количество баллов: 1Дан — отрезок CD. Требуется — построить равный ему отрезок (такой же длины). Установить последовательность шагов.
-
Построим произвольный луч с началом в новой точке А.
-
Циркулем замерим данный отрезок CD.
-
Теперь тем же самым раствором циркуля на построенном луче от его начала — A — отложим отрезок, равный данному.
-
Для этого иглой циркуля упираем в начало луча A, а пишущей ножкой проводим дугу до пересечения с лучом.
-
Точку пересечения назовём B. Отрезок AB равен данному отрезку CD.
Правильно
Неправильно
-
