Геометрия, 11класс. Метод координат в пространстве.
Навигация (только номера заданий)
0 из 14 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
Информация
Для выполнения теста необходимо повторить: векторы в пространстве; метод координат в пространстве.
УДАЧИ !
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается...
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Результаты
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Нет рубрики 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- С ответом
- С отметкой о просмотре
-
Задание 1 из 14
1.
Количество баллов: 1Точка M (–2; 3; –7) находится от плоскости XOY на расстоянии, равном…
1) 7;
2) 2;
3) 3. -
Задание 2 из 14
2.
Количество баллов: 1 -
Задание 3 из 14
3.
Количество баллов: 1 -
Задание 4 из 14
4.
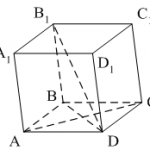
Количество баллов: 1Первая и третья координаты ненулевого вектора
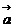 равны нулю. Выбрать номера верных утверждений.
равны нулю. Выбрать номера верных утверждений.1)
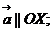 2)
2) 3)
3)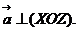
-
Задание 5 из 14
5.
Количество баллов: 1 -
Задание 6 из 14
6.
Количество баллов: 1Ордината точки А равна 3, ордината точки В равна 6. Длина отрезка АВ равна 3. Тогда прямая АВ и ось OY…
1) параллельны;
2) перпендикулярны;
3) скрещиваются. -
Задание 7 из 14
7.
Количество баллов: 1 -
Задание 8 из 14
8.
Количество баллов: 1 -
Задание 9 из 14
9.
Количество баллов: 1Дана точка А (–1; 2; 5). Тогда координаты точки – проекции точки А на ось OZ равны…
-
Задание 10 из 14
10.
Количество баллов: 1А (–1; 0; 2), В (1; –2; 3). Тогда
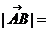 …
… -
Задание 11 из 14
11.
Количество баллов: 1ABCD – параллелограмм, В (–2; 1; 0), О (0; 1,5; 0). Тогда координаты точки D равны…
-
Задание 12 из 14
12.
Количество баллов: 1 -
Задание 13 из 14
13.
Количество баллов: 1 -
Задание 14 из 14
14.
Количество баллов: 1Какое утверждение верное?
1) Если один из трёх векторов нулевой, то векторы компланарны.
2) Если векторы компланарны, то один из них нулевой.
3) Если векторы компланарны, то они равны.